การหารพหุนาม
การหารพหุนามด้วยพหุนามทำได้โดยวิธีการตั้งหารในทำนองเดียวกันกับการหารจำนวนเต็ม ดังตัวอย่างต่อไปนี้ตัวอย่าง ต้องการหาร 2x + x2 - 3 ด้วย x + 3 ให้ทำตามขั้นตอนดังนี้
วิธีทำ
1. เรียงพจน์ของพหุนามตัวตั้งและพหุนามตัวหารจากพจน์ที่มีดีกรีมากไปพจน์ที่มีดีกรีน้อย แล้วเขียนการตั้งหารดังนี้
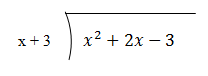
2. นำพจน์แรกของตัวหารคือ x ไปหารพจน์แรกของตัวตั้งคือ x2 จะได้ผลหารเป็น x เขียนผลหารที่ได้นี้ไว้ที่บรรทัดเหนือตัวตั้งโดยเขียนในตำแหน่งให้ตรงกับพจน์ x2 ดังนี้
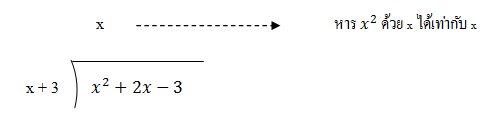
3. นำผลหารที่จากข้อ 2 คือ x ไปคูณตัวหารคือ x + 3 ได้ผลคูณเป็น x2 + 3x แล้วเขียนผลคูณที่ได้ไว้ที่บรรทัดใต้ตัวตั้ง ดังนี้
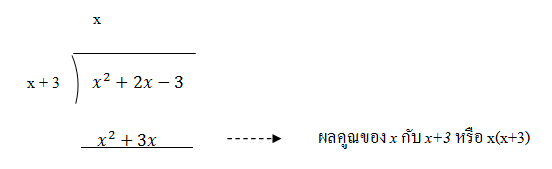
4. นำผลคูณที่ได้จากข้อ 3 คือ x2 + 3x ไปลบออกจากตัวตั้งคือ x2 + 2x - 3 จะได้ผลลบเป็น –x - 3 ดังนี้
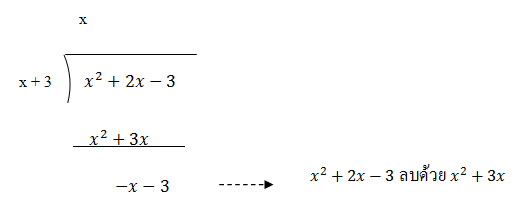
5. ผลลบที่ได้จากข้อ 4 คือ – x - 3 จะเป็นตัวตั้งใหม่ ให้ดูว่าดีกรีของตัวตั้งใหม่นี้น้อยกว่าดีกรีของตัวหารคือ x + 3 หรือไม่ ถ้าน้อยกว่าก็หยุดการหาร ถ้าไม่น้อยกว่าก็ทำการหารต่อไปอีก ในที่นี้ดีกรีของ – x - 3 ไม่น้อยกว่าดีกรีของ x + 3 จึงต้องหารต่อไป
6. นำพจน์แรกของตัวหารคือ x ไปหาพจน์แรกของตัวตั้งใหม่คือ –x จะได้ผลหารเป็น -1 นำผลหารที่ได้นี้ไปเขียนในรูปการบวกกับผลหารที่ได้ในข้อ 2 เป็น x + (-1) หรือ x - 1 แล้วทำซ้ำทำนองเดียวกันกับขั้นตอนที่ 3 และ 4 จนได้ตัวตั้งใหม่คือ พหุนาม 0 จึงหยุด ดังนี้
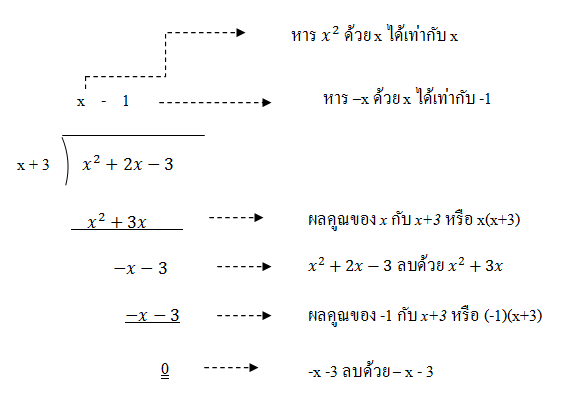
จากการหารพหุนามข้างต้น เรากล่าวว่า x2 + 2x - 3 หารด้วย x + 3 ได้ผลหารเป็น x – 1 และเศษเป็น 0 เขียนความสัมพันธ์ของตัวตั้ง ตัวหาร ผลหารและเศษ ได้ดังนี้
x2 + 2x - 3 = (x + 3)(x - 1) + 0
โดยทั่วไป ในการหารพหุนามเราเขียนความสัมพันธ์ของตัวตั้ง ตัวหาร ผลหารและเศษได้ดังนี้
ตัวตั้ง = (ตัวหาร × ผลหาร) + เศษ
เมื่อผลหารเป็นพหุนาม และเศษเป็นศูนย์หรือเป็นพหุนามที่มีดีกรีน้อยกว่าดีกรีของตัวหาร
การหารพหุนามใดได้เศษเป็นศูนย์ เรากล่าวว่าการหารพหุนามนั้นเป็น การหารลงตัว ส่วนการหารพหุนามใดได้เศษไม่เป็นศูนย์ เรากล่าวว่าการหารพหุนามนั้นเป็น การหารไม่ลงตัว
จาก x2 + 2x - 3 หารด้วย x + 3 ได้ผลหารเป็น x - 1 เศษเป็น 0 จึงกล่าวว่า การหารนี้เป็นการหารลงตัว
ไม่มีความคิดเห็น:
แสดงความคิดเห็น